Confidence Intervals

Sonia Markes

University of Toronto

August 8, 2023

Definition

Definition 1 (Confidence Interval)

Let \(\alpha\) be a number between 0 and 1.

The interval \((\ell_n, u_n)\) where \(\ell_n = g(x_1,...,x_n)\) and \(u_n = h(x_1,...,x_n)\) is called a

\(\bf{100(1-\alpha)\%}\) confidence interval for \(\bf{\theta}\)

if there exists \(L_n = g(X_1,...,X_n)\) and \(U_n = h(X_1,...,X_n)\) that satisfy

\[ \Pr(L_n < \theta < U_n)=1-\alpha \;\text{ for every value of } \theta \]

\(1-\alpha\) is the confidence level.

Features

A confidence interval is for a parameter
The parameter is not random
The bounds of a confidence interval are random
Each sample gives a different confidence interval estimate

Definition 2 (Conservative Confidence Interval)

If \[P(L_n < \theta < U_n)\geq 1-\alpha\] for every value of \(\theta\), we say the resulting confidence interval is conservative.

The actual confidence level might be higher, but \(L_n\) and \(U_n\) can only be found to give a lower bound.

Interpretation

Confidence level

Suppose \(\alpha = 0.05\). Then the confidence of level is \(95\%\).

\(95\%\) of all possible samples of data of size \(n\) will give a confidence interval that includes the “true” value of \(\theta\).
\(5\%\) of all possible samples of data of size \(n\) will give a confidence interval that does not include the “true” value of \(\theta\).

The confidence level is the probability that we get an interval that includes \(\bf{\theta}\).

Script for a confidence interval

\[ \; \]

“We are \(95\%\) confident that the true value of \(\theta\) is between between \(\ell_n\) and \(u_n\).”

\[ \; \]

When interpreting confidence intervals, always remember …

The intervals are random.
\(\bf{\theta}\) is not.

How not to interpret CI

Example: A sample of \(30\) widgets is taken off an assembly line for quality control and the diameter of each is measured. A \(95\%\) confidence interval for the mean diameter is \((10.1, 14.5)\) cm.

Which of these statements are correct?

\(95\%\) of all samples will give an average diameter between \(10.1\)cm and \(14.5\) cm.

We are \(95\%\) confident that the diameter of these \(30\) widgets is between \(10.1\)cm and \(14.5\)cm.

There is a \(95\%\) chance that the true mean diameter is between \(10.1\)cm and \(14.5\) cm.

Confidence intervals for the mean

Methods

Suppose our data \(x_1,...,x_n\) is a realization of a random sample, \(X_1, ..., X_n\), and we want to find a confidence interval for the mean, \(\mu =\mathbb{E}[X_i]\).

Using Chebyshev’s Inequality
Normal data, known variance
Normal data, unknown variance, small sample size
Unknown distribution, small sample size
Unknown distribution, large sample size

Using Chebyshev’s Inequality

Consider an unbiased estimator \(\widehat{\mu}\) that has \(\text{Var}(\widehat{\mu})=\sigma^2\).
Find a bound on the probability that \(\widehat{\mu}\) is within \(2\) standard deviations of the true mean \(\mu\).

Recall: For a random variable \(Y\) with \(\mathbb{E}[Y]=\mu_Y\) and \(\text{Var}(Y)=\sigma_Y^2\), Chebyshev’s inequality states

\[ \Pr\left( \lvert Y-\mu_Y \rvert < k\sigma_Y \right)\geq 1-\frac{1}{k^2} \]

Interpretion

\(\widehat{\mu}\) is in the interval \(({\mu}-2\sigma, {\mu}+2\sigma)\) with probability greater than \(0.75\)

\({\mu}\) is in the interval \((\widehat{\mu}-2\sigma, \widehat{\mu}+2\sigma)\) with probability greater than \(0.75\)

\(\mu \in (\widehat{\mu}-2\sigma, \widehat{\mu}+2\sigma)\) with confidence greater than 75%.

This is a very conservative interval.

Exercise 1 What is a conservative confidence interval for \(\widehat{\mu}=\bar{X}_n\) being within \(2\sigma\), where \(\mathbb{E}[X_i]=\mu\) and \(\text{Var}(X_i)=\sigma^2\)?

Normal data, known variance

Suppose \(X_1, ..., X_n \overset{iid}{\sim} \text{N}(\mu,\sigma^2)\) with known \(\sigma^2\).
Consider estimating \(\mu\) with \(\bar{X}_n\).
We want to derive the confidence interval at the \(1-\alpha\) level.

Derivation

What is the sampling distribution of \(\bar{X}_n\)? … standardized?

Confidence intervals rely on quantiles in the tails of a sampling distribution.

Definition 3 A critical value \(z_p\) of a standard normal distribution, \(\text{N}(0,1)\), is defined as the value such that

\[ \Pr(Z\geq z_p)=p \]

So \(z_p\) is the \((1-p)^{th}\) quantile of \(\text{N}(0,1)\).

For example:

qnorm(0.025, lower.tail = FALSE)

[1] 1.959964

qnorm(0.975, lower.tail = FALSE)

[1] -1.959964

\[ \Pr\left( -z_{\alpha/2} < \frac{\bar{X}_n-\mu}{\sigma/\sqrt{n}}< z_{\alpha/2} \right)=1-\alpha \]

Example 1 What is the \(95\%\) confidence interval for \(\mu\)?

Forumla

For a random sample \(X_1, ..., X_n\) such that \(X_i\overset{iid}{\sim} \text{N}(\mu,\sigma^2)\) with known \(\sigma^2\),

\[ \frac{\bar{X}_n-\mu}{\sigma/\sqrt{n}}\sim\text{N}(0,1) \]

Then the \(100(1-\alpha)\%\) confidence interval for \(\mu\) is

\[ \left(\bar{x}_n - z_{\alpha/2} \frac{\sigma}{\sqrt{n}} ,\; \bar{x}_n + z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\right) \]

Normal data, unknown variance, small sample size

Suppose \(X_1, ..., X_n \overset{iid}{\sim} \text{N}(\mu,\sigma^2)\) with unknown \(\sigma^2\).
We are interested in estimating \(\mu\) with \(\bar{X}_n\).
We can estimate \(\sigma\) by \(S_n=\sqrt{\frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X}_n)^2}\).
We want a confidence interval at the \(1-\alpha\) level.

Sampling distributions

… of \(\bar{X}_n\)?

\[ \bar{X}_n \sim \text{N}\left( \mu,\frac{\sigma^2}{\sqrt{n}} \right) \]

… of \(S_n^2\)?

\[ \sum_{i=1}^n \left( X_i -\bar{X}_n \right)^2 \sim \sigma^2 \mathcal{\chi}^2_{n-1} \]

… of \(\frac{\bar{X}_n-\mu}{S_n/\sqrt{n}}\)?

\[ \frac{\bar{X}_n-\mu}{S_n/\sqrt{n}} \sim t_{n-1} \]

Student’s t-distribution

The \(t\) distribution has one parameter, called the degrees of freedom.
\(\frac{\bar{X}_n-\mu}{S_n/\sqrt{n}}\) is called the studentized mean.

Properties

Similar to the Normal distribution
- Symmetric
- Bell-shaped
- Centred at 0
Heavier tails than the Normal distribution
- Smaller degrees of freedom have heavier tails
- Larger degrees of freedom get closer to the standard Normal distribution
- \(t(1) \sim \text{Cauchy}(0,1)\)

Plots

In R

To calculate probabilities from the CDF of the \(t\) distribution, use the function pt().

Example: \(\Pr(T > 0.5)\)

# check: equivalent to Cauchy for DoF=1
1 - pt(0.5, 1)

[1] 0.3524

1 - pcauchy(0.5)

[1] 0.3524

# check: approaches Normal for large DoF
1 - pt(0.5, 125)

[1] 0.309

1 - pnorm(0.5)

[1] 0.3085

To calculate quantiles (or critical values) from the \(t\) distribution, use the function qt(p, df).

Example: \(n=10\)

# critical values for 90% confidence interval, DoF = 10-1
qt(0.05, df = 9, lower.tail = FALSE)

[1] 1.833

# critical values for 95% confidence interval, DoF = 10-1
qt(0.025, df = 9, lower.tail = FALSE)

[1] 2.262

Formula

For a random sample \(X_1, ..., X_n\) such that \(X_i \overset{iid}{\sim} \text{N}(\mu,\sigma^2)\) with unknown \(\sigma^2\),

\[ \frac{\bar{X}_n-\mu}{S_n/\sqrt{n}}\sim t_{n-1} \]

Then the \(100(1-\alpha)\%\) confidence interval for \(\mu\) is

\[ \left(\bar{x}_n - t_{n-1,\;\alpha/2} \frac{s_n}{\sqrt{n}} ,\; \bar{x}_n + t_{n-1,\;\alpha/2} \frac{s_n}{\sqrt{n}}\right) \]

Unknown distribution, small sample size

What if the random sample is not drawn from a Normal distribution?

Bootstrap t

Suppose \(X_1, ..., X_n \overset{iid}{\sim}F\) with \(\mathbb{E}[X_i]=\mu\).
Estimate \(F\) by \(F_n\), the empirical cumulative distribution function.
The expectation corresponding to \(F_n\) is \(\bar{x}_n\). This is often written \(\mu^*\).

Input

sample \(X_1,...,X_n\)
sample average \(\bar{X}_n\)
number of bootstrap samples, \(B\)

Repeat the following for each of \(b=1,...,B\):

Sample with replacement from \(X_1,...,X_n\) to obtain a bootstrap sample \(X_1^*,...,X_n^*\)
Compute the mean and standard deviation of the bootstrap sample, \(\bar{X}_n^*\) and \(s_n^*\) respectively.
Compute \(T_{n,b}^*=\frac{\bar{x}^*_n-\bar{x}}{s_n^*/\sqrt{n}}\)

Output

\(T_{n,1}^*, ..., T_{n,B}^*\)

The sample quantiles of \(T_{n,1}^*, ..., T_{n,B}^*\) can be used in place of the theoretical quantiles in a confidence interval.
Let \(c_l^*\) and \(c_u^*\) be the \(\alpha/2\) and \(1-\alpha/2\) quantiles from the bootstrap distribution.

Formula

For \(X_1, ..., X_n \overset{iid}{\sim}F\) with \(\mathbb{E}[X_i]=\mu\),

\[ P\left( c_l^* < \frac{\bar{X}_n^* - \mu^*}{S_n^*/\sqrt{n}}< c_u^* \right) \approx 1-\alpha \]

Then the \(100(1-\alpha)\%\) bootstrap confidence interval for \(\mu\) is

\[ \left(\bar{x}_n - c_u^* \frac{s_n}{\sqrt{n}} ,\; \bar{x}_n - c_l^* \frac{s_n}{\sqrt{n}}\right) \]

Unknown distribution, large sample size

Consider estimating \(\mu\) with \(\bar{X}_n\).
We want to derive the confidence interval at the \(1-\alpha\) level.

By CLT

For large \(n\), the sampling distribution of \(\bar{X}_n\) is approximately Normal.

\[ \frac{\bar{X}_n-\mu}{\sqrt{\text{Var}(X_i)/ n}}\sim\text{N}(0,1) \]

Estimate \(\text{Var}(X_i)\) with \(S_n^2\).

How does this relate to the studentized mean?

Formula

Suppose the data \(x_1,...,x_n\) are realizations of a random sample \(X_1, ..., X_n\), drawn from a distribution with cdf \(F\) and expectation \(\mu\).

If \(n\) is large, then the approximate \(100(1-\alpha)\%\) confidence interval for \(\mu\) is

\[ \left(\bar{x}_n - z_{\alpha/2} \frac{s_n}{\sqrt{n}} ,\; \bar{x}_n + z_{\alpha/2} \frac{s_n}{\sqrt{n}}\right) \]

CIs for the mean

If \(X_i\sim \text{Normal}\), \(\text{Var}(X_i)=\sigma^2\):

\[ \bar{x}_n \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \]

If \(X_i\sim \text{Normal}\), \(\widehat\sigma=S_n\):

\[ \bar{x}_n \pm t_{n-1,\;\alpha/2} \frac{s_n}{\sqrt{n}} \]

If \(n\) is large:

\[ \bar{x}_n \pm z_{\alpha/2} \frac{s_n}{\sqrt{n}} \]

If unsure:

… bootstrap.

Interpretation, revisited

Simulation

This will give us an idea of how confidence intervals can vary with the data.

We will generate data from a known distribution and compute the confidence intervals for the mean.
Repeat for many datasets drawn from the same distribution.

Set values

Generate \(95\%\)-confidence intervals for \(200\) datasets, each a sample size of \(20\) drawn from a \(N(10,4)\) distribution.

set.seed(238)

# Sample size 
n <- 20

# Number of repeated samples 
B <- 200

# Set parameters of theoretical world distribution
mu <- 10
sigma <- 4

# Use confidence level 1-alpha
alpha <- 0.05

# Critical value from a standard normal distribution
critval <- qnorm(1-alpha/2)

Generate

# Store the CI limits for B samples 
CIs <- tibble("sampmean" = numeric(B),
                   "lowerlimit" = numeric(B), 
                   "upperlimit" = numeric(B))

# Generate confidence intervals
for (i in 1:B){
  sampdata <- rnorm(n, mu, sigma)
  CIs[i,1] <- mean(sampdata)
  CIs[i,2] <- mean(sampdata) - critval*sigma/sqrt(n)
  CIs[i,3] <- mean(sampdata) + critval*sigma/sqrt(n)
}

# Display first 5 rows
head(CIs, 5)

# A tibble: 5 × 3
  sampmean lowerlimit upperlimit
     <dbl>      <dbl>      <dbl>
1     9.27       7.52       11.0
2    11.2        9.42       12.9
3    11.9       10.1        13.6
4     9.48       7.72       11.2
5    10.9        9.14       12.6

Check

With interval estimates, we are trying to “capture” \(\mu=10\).
However, we expect that the proportion of intervals to not contain \(\mu\) would be \(\alpha\).

# Percentage of confidence intervals to *not* contain mu
( sum(CIs$lowerlimit > mu) + sum(CIs$upperlimit < mu) ) / B

[1] 0.05

Would that work out so perfectly for every set of samples? What about smaller sample size?

B1 <- 50
CIs1 <- CIs %>% 
  mutate(x = row_number()) %>% 
  filter(x <= B1)
# Percentage of confidence intervals to *not* contain mu
( sum(CIs1$lowerlimit > mu) + sum(CIs1$upperlimit < mu) ) / B1

[1] 0.08

Plot

Plot the first \(50\) confidence intervals, along with the sample mean for each.

CIs1 %>% 
  ggplot(aes(x = x)) +
  theme_classic() +
  geom_errorbar(aes(ymin = lowerlimit, ymax = upperlimit), color = "grey40") +
  geom_point(aes(y = sampmean), colour = "black", size = 0.7) +
  geom_hline(yintercept = mu, color = "blue") +
  #coord_flip() +
  labs(y = "", x="")

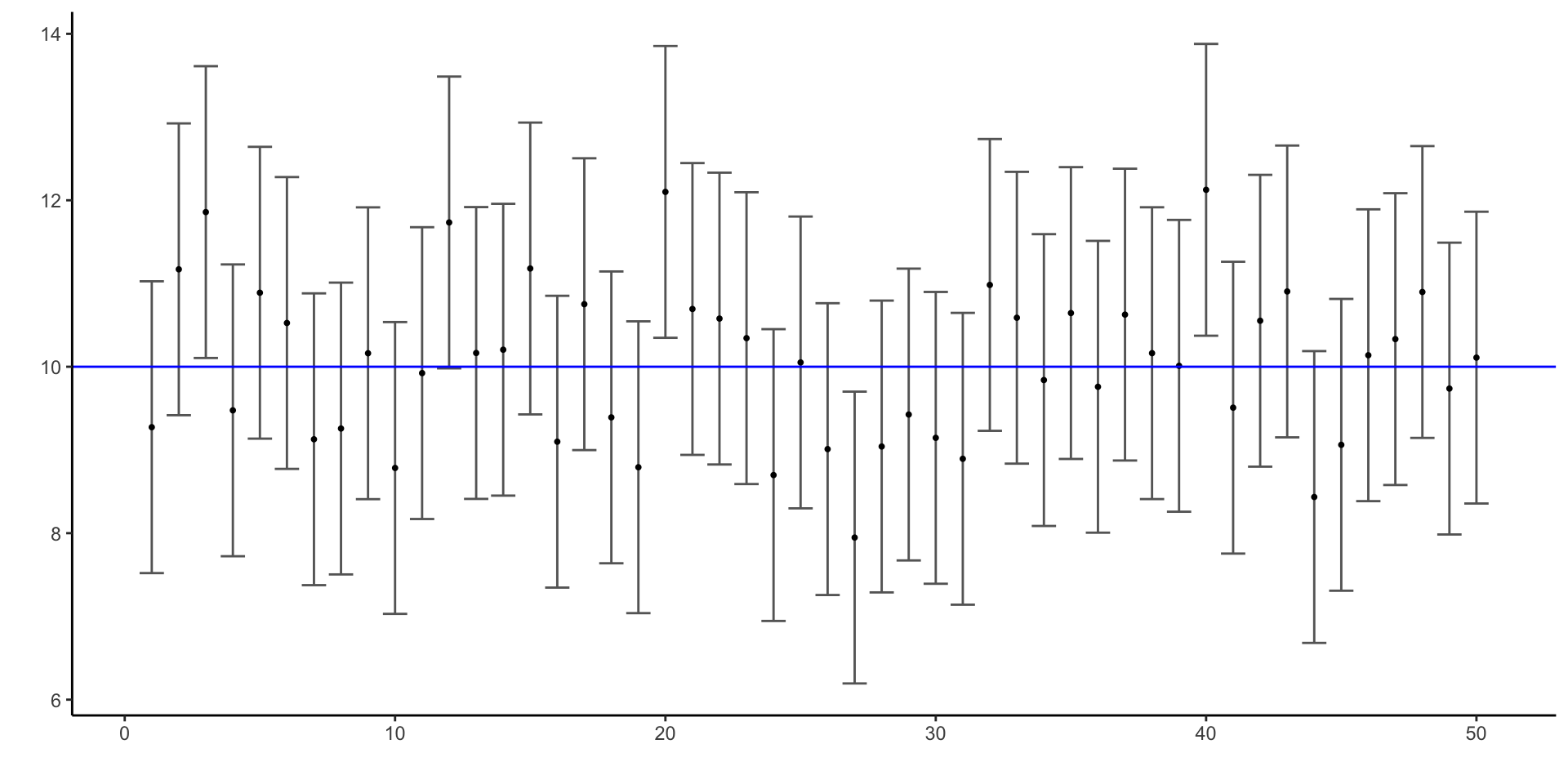
How do the intervals change for smaller (or larger) values of \(\alpha\)?

Other methods for CIs

Proportions

Consider a random sample \(X_1,...,X_n\) where \(X_i \sim Bernoulli(p)\).
Let \(Y=\sum_{i=1}^n X_i\) represent the number of successes and \(Y\sim Binomial(n,p)\).
Consider the estimator \(\widehat{p}=\frac{Y}{n}\).
Can we find a confidence interval for \(p\)?

What is the sampling distribution of \(\widehat{p}\)?

\[ \; \]

How can we use this sampling distribution to find a confidence interval?

Exercise 2 Poll 955 people and 0.46 of respondents say they would vote for your candidate. Could your candidate get a majority of votes?

Pivots

Suppose we have data \(x_1,...,x_n\) which are realizations of a random sample \(X_1, ..., X_n\).
We want to find a \(100(1-\alpha)\)% confidence interval for a parameter \(\theta\).

Definition

If we can find another random variable that

depends on \(X_1, ..., X_n\) and \(\theta\), and
whose probability distribution does not depend on \(\theta\) or any other unknown parameters,

then we can construct a confidence interval.

Random variables that satisfy these criteria are called pivots.

Example 2 Say we have a random sample \(X_1, ..., X_n\overset{iid}{\sim}\text{N}(\mu,\sigma^2)\), but we do not know \((\mu,\sigma^2)\). We want a confidence interval for \(\mu\).

Then

\[ h(X_1,...,X_n|\mu)=\frac{\overline{X}_n-\mu}{S_n/\sqrt{n}} \]

is a pivot, because \(h(X_1,...,X_n|\mu)\sim t_{n-1}\) does not depend on any unknown parameters.

Example 3 Say we have a random sample \(X_1, ..., X_n\overset{iid}{\sim}\text{N}(\mu,\sigma^2)\), but we do not know \((\mu,\sigma^2)\). We want a confidence interval for \(\sigma\).

Recall: \[ (n-1)S_n^2=\sum_{i=1}^n \left( X_i -\bar{X}_n \right)^2 \sim \sigma^2 \cal{\chi}^2_{n-1} \]