Estimators, Part 2

Sonia Markes

University of Toronto

July 17, 2023

Evaluating Estimators

Part 1

• Bias
• Consistency

Part 2

• Efficiency
• Mean Squared Error

Efficiency

Given \(\widehat\theta_1\) and \(\widehat\theta_2\) are two unbiased, consistent estimators for \(\theta\), which would be prefer to use?

It may be preferable to choose the one that varies the least.

The estimator with the smaller variance is said to be more efficient.

Definitions

If \(\widehat\theta_1\) and \(\widehat\theta_2\) are both unbiased estimators for \(\theta\), then

• \(\widehat\theta_2\) is more efficient than \(\widehat\theta_1\) if \(\text{Var}(\widehat\theta_2) < \text{Var}(\widehat\theta_1)\) irrespective of the value of \(\theta\).

• The relative efficiency of \(\widehat\theta_2\) with respect to \(\widehat\theta_1\)cc is \(\frac{\text{Var}(\widehat\theta_1)}{\text{Var}(\widehat\theta_2)}\)

Example 1 Given \(X_1, ...,X_n\) iid with \(\mathbb{E}[X_i]=\mu\) and \(\text{Var}(X_i)=\sigma^2\). Which of these unbiased¹ estimators of \(\mu\) is preferred? \[ \begin{align*} \widehat\mu_1 = \bar{X} && \widehat\mu_2 = X_1 \end{align*} \]

1. See: Estimators, Part 1, Example 3

Example 2 Given \(X_1, ...,X_n \overset{iid}{\sim} \text{U}[0,\theta]\). Which of these unbiased¹ estimators of \(\theta\) is preferred?

\[ \begin{align*} \widehat\theta_1 = \frac{n+1}{n}X_{(n)} && \widehat\theta_2 = 2 \bar{X} \end{align*} \]

Recall: For \(X_i \sim \cal{U}[0,\theta]\),

\[ f(x|\theta)= \begin{cases} \frac{1}{\theta} &\text{for } 0 \leq x \leq \theta \\ 0 &\text{otherwise } \end{cases} \] \[ \text{E}[X_i]=\frac{\theta}{2} \] \[ \text{Var}(X_i)=\frac{\theta^2}{12} \]

1. See: Estimators, Part 1, Example 5 for \(\widehat\theta_1\). Showing that \(\widehat\theta_2\) is unbiased is left as a exercise.

Is there a best estimator?

The Cramér-Rao lower bound tells us how small the variance of an unbiased estimator can be.

\[ \text{Var}(\widehat\theta) \geq \frac{1}{n\mathbb{E}\left[ \left( \frac{\partial}{\partial \theta} \ln f_\theta (X)\right)^2\right]} \]

These are called minimum variance unbiased estimators.

How could we do better than minimum variance and unbiased?

Mean Squared Error

Quantifies the difference between an estimator and an estimand, accounting for both bias and variance.

Definition

Let \(\widehat\theta\) be an estimator for a parameter \(\theta\). The mean squared error of \(\widehat\theta\) is

\[ MSE(\widehat\theta)=\text{E}\big[(\widehat\theta-\theta)^2 \big] \]

Proposition 1 If \(\widehat\theta\) is unbiased, then \(MSE(\widehat\theta) = \text{Var}(\widehat\theta)\).

Proposition 2 If \(\widehat\theta\) is any estimator \(\widehat\theta\) for \(\theta\), then \(MSE(\widehat\theta)=\text{Var}(\widehat\theta)+\text{Bias}_{\widehat\theta}^2\).

Bias-Variance Tradeoff

In estimation

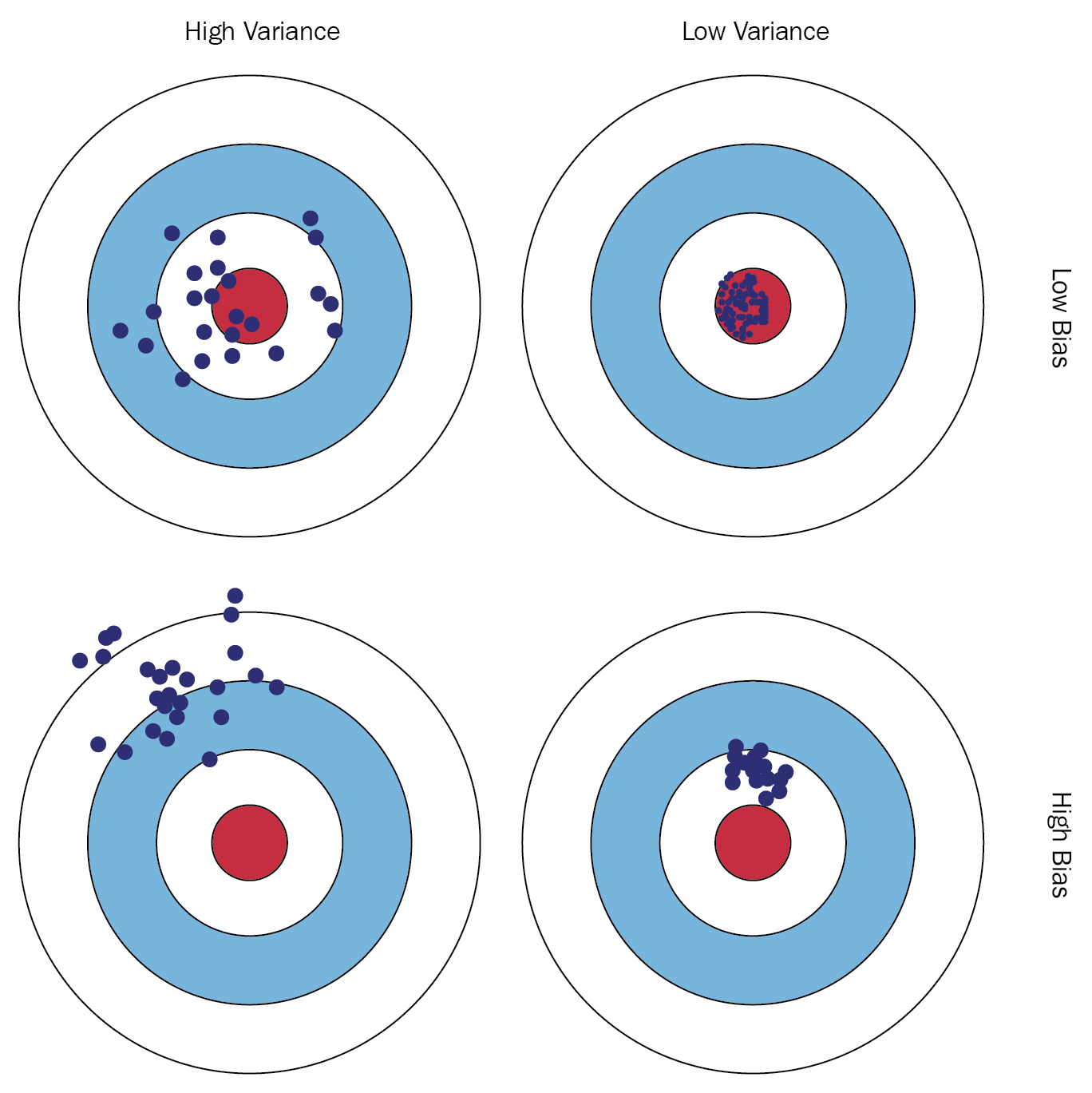
Bias-Variance Tradeoff

In models